廣義線性回歸 General Linear Regression

承接上篇文章，本文將繼續介紹廣義線性回歸模型，接續介紹模型的迴歸係數與參數估計。

回歸係數 Regression Coefficient

回歸係數為回歸模型的參數估計值。以剛剛的例子做說明，Beta0 = 24 代表當 X1 = X2 = 0 時，EY = 24。Beta1 = 1 代表當 X2 固定時，X1 每增加 1 單位，則 EY 隨之增加 1 單位；Beta2 = 2 同理。在此，　Beta1, Beta2 為當其他解釋變數不變時，該參數對應的解釋變數對反應變數的影響 ，稱作偏迴歸係數（partial regression coefficient）。

估計回歸係數

利用最小平方法估計廣義線性回歸模型的迴歸係數。廣義線性回歸模型的誤差平方合為

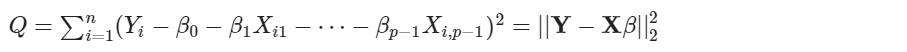
接下來要找尋一組 Beta 的值，使得 Q 最小。所以設

為最小平方法所估計的迴歸係數向量，則 Q 的最小平方正規方程式（normal equations）為

而其最小平方法解，同時也是參數之最小平方法估計量為

最後，回歸模型擬合值為

殘差項

配適模型後，還需要檢查模型殘差項是否符合當初的模型假設。設殘差項 ei = Yi - Yi hat ，則殘差項向量

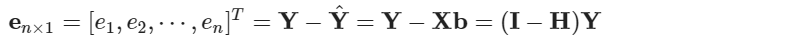
其中 hat matrix

而殘差的 variance-covariance 矩陣

為 n 階方陣。

參考資料：
Michael H. Kutner, Christopher J. Nachtsheim, John Neter, and William Li (2019), Applied Linear Statistical Models. McGraw Hill, New York.

正規方程式解二次式可參考：

• The normal equations
• Normal Equation（正規方程式）